예제를 볼때는 트리를 이용해서 DFS/BFS 탐색 이론을 배운다.
그리고 다음과 같은 예제 보고 "각자 BFS/DFS 탐색 방식 구현해보는 실습하세요~"라고 하면 멘붕
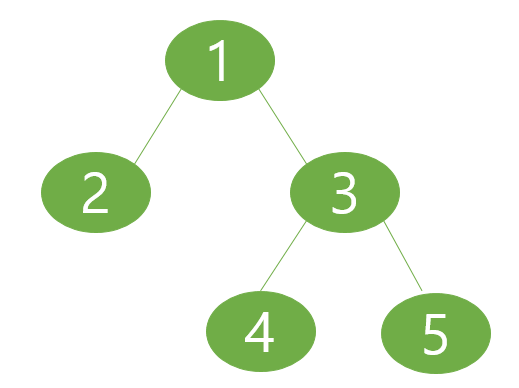
이론을 알겠는데, 막상 구현해볼라하면 어떻게 하지? 라는 생각이 든다.
(수업할때 나 빼고 다 아는것 같았음.. 난 몰랐어서 정리 ㅎ)
일반적으로 트리를 표현할 때에는 인접행렬 혹은 인접리스트 이렇게 2가지 방식으로 구현한다.
1. 인접행렬
인접행렬? 말 그대로다. 2차원 배열로 구현하는 것이다.

int[][] arr = {{0,1,1,0,0}, {1,0,0,0,0}, {1,0,0,1,1}, {0,0,1,0,0}, {0,0,1,0,0}};너무 당연한가? ㅋㅋㅋㅋㅋ (1,1)~(5,5) 대각선 기준으로 대칭이 되는 것을 볼 수 있다.
2. 인접리스트
인접리스트는 그래프를 이용하여 구현한다. 인접 행렬에 비해 눈으로 보고 이해하기 더 쉽다. (개인적인 의견임)
package java_BFS_DFS_basic;
import java.util.LinkedList;
/*
* DFS - 그래프를 이용하여 구현
* 그래프 구현방법 - 인접행렬 / 인접리스트 방식 중
* 인접리스트를 이용하여 구현
*/
public class Graph {
private LinkedList<Integer>[] adj; //인접 리스트 생성
private int v; //vertex - 정점
// 그래프 생성 및 초기화
Graph(int v){
this.v = v; //정점 개수 초기화
//visit = new boolean[v]; // 체크를 위한 값 생성
adj = new LinkedList[v+1]; // v로 하면 0부터 시작하니까, 보기 쉽게 1부터함. 0은 공백으로 둠
//인접리스트 초기화 작업
for(int i=0; i<v+1; i++) {
adj[i] = new LinkedList();
}
}
// 그래프 인자끼리 연결하기
void addEdge(int v1, int v2) {
adj[v1].add(v2);
adj[v2].add(v1);
}
public static void main(String args[]) {
Graph dfs_g = new Graph(5);
dfs_g.addEdge(1, 2);
dfs_g.addEdge(1, 3);
dfs_g.addEdge(3, 4);
dfs_g.addEdge(3, 5);
//인자값 1부터 출력
for(int i=1; i<dfs_g.adj.length; i++) {
System.out.println(i+" : "+dfs_g.adj[i]);
}
}
}
출력결과 :
1 : [2, 3]
2 : [1]
3 : [1, 4, 5]
4 : [3]
5 : [3]
코딩 테스트에서 구현할때는 주로 행렬 형태로 많이 주니까, 행렬로 연습하는 것이 좋을 듯 싶다.
근데 최단경로 간선에 값이 추가된다면 인접리스트로 구현하고 푸는것이 나을수도 있다는 생각이듬
아무튼 방법은 2가지 이고, 경우에 따라 효율적이라고 생각하는 방식으로 만들어서 풀면 될 듯 하다.
'알고리즘 공부 > 알고리즘 개념' 카테고리의 다른 글
| Kruskal (크루스칼) 알고리즘 (0) | 2019.05.31 |
|---|---|
| Union Find 알고리즘 (0) | 2019.05.29 |
| DFS 알고리즘 (2) - 예제(행렬의 영역 구하기) (0) | 2019.04.08 |
| DFS 알고리즘 (1) - 이론 (0) | 2019.04.08 |
| 삽입 /선택 / 버블 정렬 JAVA로 구현하기 (0) | 2019.03.12 |